
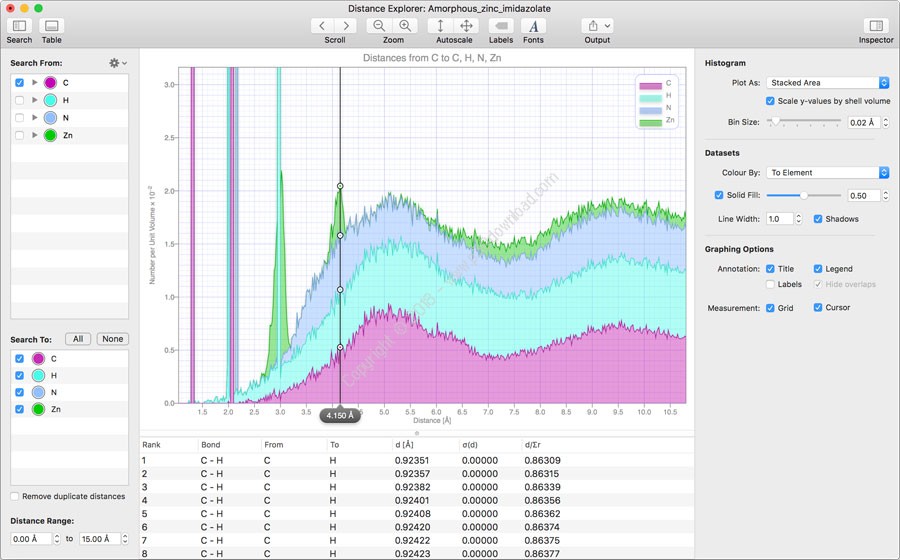
I would highly recommend to read one of the well availabel books about this topic. by sample preparation (textured materials), since there are also other effects influencing the intensity of relactions (except of the relative atomic positions in the unit cell). But also the structure information (intensity) can be falsified, i.e. This combination often works with JCPDS quite nicely, but with specific uncertainties since often phases are not really chemically ideal. Then only the intensity can distinguish between both phases. So it is possible to generate phases with a lattice with identical (or pseudo-symmetrical) parameters so that the reflex positions of both phases are absolutely identical. The other information is related to the crystal STRUCTURE (relatice position of atoms within the unit cell) which mainly effects whether a reflex becomes visible or not, i.e. Small changes in composition will change the peak positions even if the distribution of atoms keeps unchanged. The Bragg angles (or d-values) are related to the the crystal LATTICE. or a well defined double-peak.Īlthough it has been written in other answers to other questions many time I want repeat it briefly: The JCPDS supports you with different information. In so far it does not make any (remarkable) difference with which profile you are analysing the diffractogram: a single profile of a Gausian, a Voigtian etc. A deconvolution does not give you any remarkable advantage since all dependencies are valid for all pea in the same way. The radiation doublet splitting is not problematic since all programs use a refinement procedures considering this behavior. One is PowderCell, but I am sure that also MAUD or Fullprof export these data.
OFFSETTING ORIGIN IN CRYSTALMAKER SOFTWARE
To get a FWHM description I am sure that many software packages deliver U, V and W (Caglioti formula) in order to describe the FWHM variation as function of theta. I myself prefer the fundamental approach which also considers focus size, wave length distribution incl. with specific grain size distributions which won't contribute any remarkable broadening) and a sample preparation which does not cause any lattice strain in first approach the profiles reflect the instrumental broadening. I don't know another software which is doing this but it might be that there are some other programs using this fundamental parameters approach.
OFFSETTING ORIGIN IN CRYSTALMAKER FULL
BGMN (a Rietveld and full pattern refinement software) derives from the geometrical conditions this function by ray-tracing.
The instrumental broadening you actually cannot get from a sample (standard or not) since the result also contains the impact of the sample investigated. But the observed interference can be also caused by another phase. Of course there are several other SiO2 phases which might have a translation lattice where one specific plane has a better matching distance. SiO2 (quartz) does not since the closest distance of a lattice plane is about 3.3 angstroem which generates an interference at 26.6 degrees. For Si there is a lattice plane which fulfills this condition. If you want decide about the ability to generate such an interference you only need to check the translation lattice of the respective phase. Therefore an unequivocal answer on your question is impossible. And any phase which has a lattice plane distance of about 3.1 angstroem (anyway which indexing and lattice parameters or symmetry) will produce a reflection at this position. This angle only tells you that there is a lattice distance d=3.1 angstroem which generates this diffraction. You cannot simply ask for a peak at 28 degree and which phase is related to this interference.


 0 kommentar(er)
0 kommentar(er)
